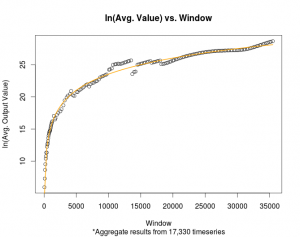
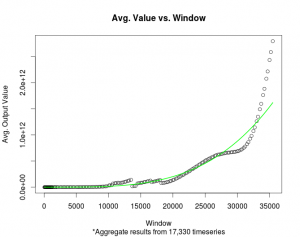
On December 20th, 23rd, and 29th The Bubble Index: Bitcoin/USD 52, 104, and 153 day indices, respectively, peaked. This means that the derivative reached zero and indicates that the phase-change probability would be highest in 21 days. Thus, on January 7th I predicted that we will see a phase change in 21 days from the point of those local peaks. In other words, the greatest probability for a phase change would occur between the days January 9th and 18th. There was some personal uncertainty because the longer term indices (512 – 1764 day indices) had yet to reach a local peak.
At its height, the Bitcoin/USD exchange rate was around $19700 on December 17, 2017. When the 52, 104, and 153 day indices peaked the exchange rate closed at $17340, $13174, and $14323.
Looking at the exchange rate data after January 7th, the most noticeable movement was the large draw-down which started on January 6th and still continues. If we look at the closing rate on January 9th: $14920 and compare it to $8317, the price at its low on February 2nd, we see a draw-down of 44.26%.
Based on this draw-down I would conclude that the prediction on January 7th, based solely on The Bubble Index’s quantitative output, was accurate and it remains to be seen what will happen to the Bitcoin/USD exchange rate, now that the longer term indices have peaked. My personal opinion is that the rate will continue its downward progression until it reaches significant support, perhaps at the $6000 or $4000 level.